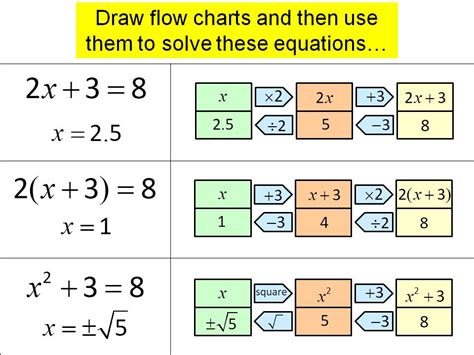
Understanding inverse operations is a fundamental concept in mathematics, crucial for solving equations and simplifying expressions. In essence, inverse operations are pairs of operations that "undo" each other. For instance, addition and subtraction are inverse operations, as are multiplication and division. Mastering the concept of inverse operations can significantly simplify mathematical problem-solving, making it easier to isolate variables in equations or simplify complex expressions. In this article, we will delve into the simplified steps for finding inverse operations, exploring their application in various mathematical contexts.
Key Points
- Understanding the concept of inverse operations as pairs of operations that reverse each other.
- Identifying inverse operations for basic arithmetic operations: addition/subtraction and multiplication/division.
- Applying inverse operations to solve linear equations and simplify algebraic expressions.
- Using inverse operations in real-world applications, such as calculating percentages and understanding financial transactions.
- Developing problem-solving strategies that incorporate inverse operations for efficient and accurate solutions.
Introduction to Inverse Operations

Inverse operations are mathematical operations that reverse the effect of each other. For example, if we have an equation like x + 5 = 11, to solve for x, we need to perform the inverse operation of addition, which is subtraction. Thus, subtracting 5 from both sides gives us x = 11 - 5, simplifying to x = 6. Similarly, for multiplication and division, if we have 4x = 20, dividing both sides by 4 gives us x = 20 / 4, which simplifies to x = 5. Understanding these inverse relationships is key to manipulating and solving equations.
Identifying Inverse Operations
Identifying inverse operations involves recognizing the pairs of operations that cancel each other out. The primary inverse operations are:
- Addition and Subtraction: These are inverse operations because they cancel each other out. For example, 3 + 4 - 4 = 3.
- Multiplication and Division: These operations are inverses of each other because multiplying a number by its reciprocal (1 divided by the number) equals 1. For example, 4 * (1⁄4) = 1.
These basic inverse operations are the foundation for more complex mathematical manipulations, including solving equations and simplifying expressions.
Applying Inverse Operations

The application of inverse operations is crucial in algebra and arithmetic for solving equations and simplifying expressions. Here are the steps to apply inverse operations:
- Identify the Operation: Determine the operation applied to the variable or the value you are trying to isolate. This could be addition, subtraction, multiplication, or division.
- Apply the Inverse Operation: Once the operation is identified, apply its inverse to both sides of the equation to maintain equality. For addition, the inverse is subtraction, and for multiplication, the inverse is division.
- Simplify the Expression: After applying the inverse operation, simplify the resulting expression to find the value of the variable or to simplify the equation.
This process is fundamental in solving linear equations and can be extended to more complex equations and expressions.
Real-World Applications
Inverse operations have numerous real-world applications, from calculating percentages and understanding financial transactions to solving problems in physics and engineering. For instance, understanding how to apply inverse operations can help in calculating the original price of an item after a discount or in determining the rate of increase or decrease in a quantity over time.
| Operation | Inverse Operation | Example |
|---|---|---|
| Addition | Subtraction | x + 3 = 7 becomes x = 7 - 3 |
| Multiplication | Division | 2x = 12 becomes x = 12 / 2 |

Conclusion and Future Implications
In conclusion, inverse operations are a fundamental concept in mathematics that can simplify problem-solving and expression simplification. By understanding and applying inverse operations, individuals can develop a deeper appreciation for mathematical structures and improve their ability to solve complex problems. As mathematics continues to evolve and play a critical role in various fields, from science and technology to finance and social sciences, the importance of inverse operations will only continue to grow. Thus, mastering inverse operations is not just about solving equations; it’s about developing a versatile toolset for tackling a wide range of mathematical and real-world challenges.
What are inverse operations in mathematics?
+Inverse operations are pairs of operations that reverse the effect of each other. The main inverse operations are addition and subtraction, and multiplication and division.
How do you apply inverse operations to solve equations?
+To apply inverse operations, first identify the operation applied to the variable, then apply its inverse to both sides of the equation to maintain equality, and finally simplify the resulting expression.
What are some real-world applications of inverse operations?
+Inverse operations have applications in calculating percentages, understanding financial transactions, and solving problems in physics and engineering, among others.