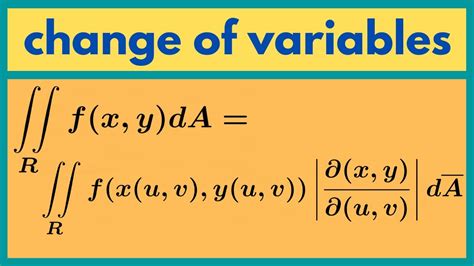The change of variables is a fundamental technique in calculus, used to simplify complex integrals by transforming them into more manageable forms. This method involves substituting a new variable or set of variables into the original integral, allowing for a more straightforward evaluation process. In this article, we will delve into the world of change of variables, exploring its applications, benefits, and step-by-step solutions to common problems.
Understanding the Basics of Change of Variables

To apply the change of variables, one must first understand the underlying concept. The technique involves introducing a new variable, say u, which is a function of the original variable x. The transformation u = f(x) is then used to substitute x in the original integral, resulting in a new integral in terms of u. The key to this method lies in finding the appropriate substitution that simplifies the integral, making it easier to evaluate.
Choosing the Right Substitution
Selecting the correct substitution is crucial in applying the change of variables. The choice of u should be based on the form of the integral, with the goal of simplifying the expression as much as possible. Common substitutions include u = x^2, u = \sin(x), or u = e^x, among others. The substitution should be chosen such that it simplifies the integrand, making it easier to integrate.
| Substitution | Derivative |
|---|---|
| $u = x^2$ | $du = 2x dx$ |
| $u = \sin(x)$ | $du = \cos(x) dx$ |
| $u = e^x$ | $du = e^x dx$ |

Applying the Change of Variables Formula

Once the substitution has been chosen, the change of variables formula can be applied. The formula states that \int f(x) dx = \int f(g(u)) \cdot g'(u) du, where x = g(u) and dx = g'(u) du. This formula allows us to transform the original integral into a new integral in terms of u, which can then be evaluated using standard integration techniques.
Step-by-Step Solution to a Common Problem
Consider the integral \int \sqrt{1 + x^2} dx. To evaluate this integral, we can use the substitution u = x^2 + 1, which simplifies the integrand. The derivative of u is du = 2x dx, which can be used to substitute dx in the original integral.
The resulting integral is $\int \sqrt{u} \cdot \frac{1}{2x} du$. To complete the substitution, we need to express $x$ in terms of $u$. Using the relation $u = x^2 + 1$, we can solve for $x$ to get $x = \sqrt{u - 1}$. Substituting this expression into the integral, we get $\int \sqrt{u} \cdot \frac{1}{2\sqrt{u - 1}} du$.
This integral can be simplified further by combining the square roots, resulting in $\int \frac{u}{2\sqrt{u - 1}} du$. This integral can then be evaluated using standard integration techniques, such as substitution or integration by parts.
Key Points
- Choose a substitution that simplifies the integrand
- Apply the change of variables formula to transform the integral
- Express the original variable in terms of the new variable
- Simplify the resulting integral and evaluate using standard techniques
- Verify the result by checking the units and physical consistency
Advanced Applications of Change of Variables
The change of variables is not limited to simple integrals. It can be used to evaluate complex integrals, such as double or triple integrals, by transforming the coordinates or variables. This technique is particularly useful in physics and engineering, where complex integrals arise in the study of phenomena such as electromagnetism, fluid dynamics, and thermodynamics.
Example: Evaluating a Double Integral using Change of Variables
Consider the double integral \int \int \frac{1}{x^2 + y^2} dx dy over the region x^2 + y^2 \leq 1. To evaluate this integral, we can use the substitution x = r \cos(\theta) and y = r \sin(\theta), which transforms the coordinates from Cartesian to polar.
The resulting integral is $\int \int \frac{1}{r^2} \cdot r dr d\theta$, which can be simplified and evaluated using standard integration techniques. The substitution simplifies the integrand and allows for a more straightforward evaluation of the integral.
What is the main goal of using the change of variables technique?
+The main goal of using the change of variables technique is to simplify complex integrals by transforming them into more manageable forms, making it easier to evaluate and solve the integral.
How do I choose the right substitution when applying the change of variables?
+Choose a substitution that simplifies the integrand, making it easier to integrate. Consider common substitutions such as $u = x^2$, $u = \sin(x)$, or $u = e^x$, and select the one that best fits the form of the integral.
Can the change of variables technique be used for double or triple integrals?
+Yes, the change of variables technique can be used for double or triple integrals. It is particularly useful in transforming coordinates or variables, making the integral more manageable and easier to evaluate.
Meta Description: Learn how to apply the change of variables technique to simplify complex integrals and make them easier to evaluate. Discover the benefits and step-by-step solutions to common problems.