The concept of root mean square (RMS) velocity is a fundamental principle in physics, particularly in the fields of thermodynamics and kinetics. It represents the square root of the mean of the squares of the velocities of the particles in a system. In essence, RMS velocity provides a measure of the average velocity of particles in a gas, considering the three-dimensional nature of their motion.
Derivation of the RMS Velocity Formula

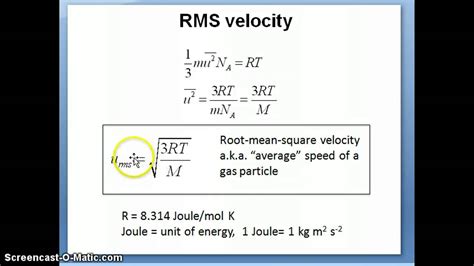
The formula for RMS velocity is derived from the kinetic theory of gases, which describes the behavior of gases in terms of the motion of their constituent particles. The RMS velocity (vRMS) of a gas is given by the equation:
vRMS = √(3RT/M)
where:
- R is the gas constant (approximately 8.3145 J/mol·K)
- T is the temperature of the gas in Kelvin
- M is the molar mass of the gas in kilograms per mole (kg/mol)
Significance of RMS Velocity
RMS velocity is significant because it allows us to understand the thermal motion of particles in a gas. At a given temperature, the RMS velocity of the particles in a gas is directly related to their thermal energy. This concept is crucial in understanding various phenomena, such as the behavior of gases under different conditions, the rates of chemical reactions, and the properties of materials.
| Gas | Molar Mass (kg/mol) | RMS Velocity at 298 K (m/s) |
|---|---|---|
| Oxygen (O2) | 0.0319988 | 483.36 |
| Nitrogen (N2) | 0.0280134 | 510.48 |
| Helium (He) | 0.0040026 | 1374.59 |
Calculating RMS Velocity

To calculate the RMS velocity of a gas, one can use the formula vRMS = √(3RT/M). For instance, to find the RMS velocity of oxygen (O2) at 25°C (298 K), we can substitute the given values into the formula:
vRMS = √(3 * 8.3145 J/mol·K * 298 K / 0.0319988 kg/mol) = 483.36 m/s
This calculation provides the RMS velocity of oxygen molecules at room temperature, illustrating how the formula can be applied to determine the thermal motion of particles in a gas.
Key Points
- The RMS velocity formula is vRMS = √(3RT/M), where R is the gas constant, T is the temperature in Kelvin, and M is the molar mass of the gas.
- RMS velocity is a measure of the average velocity of particles in a gas, considering their three-dimensional motion.
- The RMS velocity increases with the square root of the temperature, indicating that particles move more rapidly at higher temperatures.
- Understanding RMS velocity is crucial for comprehending the behavior of gases and their properties.
- The calculation of RMS velocity involves substituting the given values into the formula, as demonstrated with the example of oxygen at room temperature.
Applications of RMS Velocity
The concept of RMS velocity has numerous applications in physics, chemistry, and engineering. It is used to:
- Predict the rates of chemical reactions, as the collision frequency and energy of particles influence reaction kinetics.
- Understand the properties of materials, such as their thermal conductivity and viscosity, which are related to the motion of particles.
- Design and optimize systems, like heat exchangers and engines, where the thermal motion of particles plays a critical role in energy transfer and efficiency.
In conclusion, the RMS velocity formula provides a fundamental understanding of the thermal motion of particles in a gas. By applying this concept, we can gain insights into various phenomena and design more efficient systems.
What is the significance of RMS velocity in understanding gas behavior?
+RMS velocity is significant because it allows us to understand the thermal motion of particles in a gas, which is essential for predicting the behavior of gases under different conditions.
How does the RMS velocity of a gas change with temperature?
+The RMS velocity of a gas increases with the square root of the temperature, indicating that particles move more rapidly at higher temperatures.
What are some applications of RMS velocity in physics and engineering?
+RMS velocity has numerous applications in physics, chemistry, and engineering, including predicting the rates of chemical reactions, understanding the properties of materials, and designing and optimizing systems.

